Topology sheds new light on synchronization in higher-order networks
Like an orchestra playing in time without a conductor, the elements of a complex system can naturally synchronize with each other. This collective phenomenon, known as synchronization, occurs throughout nature, from neurons firing together in the brain to fireflies flashing in unison in the dark.
The Kuramoto model is used to study synchronization observed in complex systems. Complex systems are often mathematically represented by networks, where components in the system are represented as nodes, and the links between nodes show interactions between them.
Most studies of synchronization have focused on networks, where nodes host dynamic oscillators that behave like clocks, and couple with their neighbours along with the links of the network. However, the vast majority of complex systems have a richer structure than networks and include ‘higher-order’ interactions that occur between more than two nodes. These higher-order networks are called simplicial complexes and have been studied extensively by Mathematicians working in discrete topology.
Now, research led by Professor Ginestra Bianconi, Professor of Applied Mathematics at Queen Mary University of London, proposes a novel ‘higher-order’ Kuramoto model that combines topology with dynamical systems and characterises synchronization in higher-order networks for the first time.
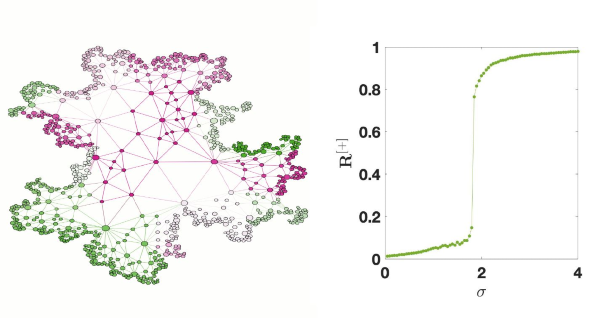
The study found that higher-order synchronization occurs abruptly, in an “explosive” way, which differs from the standard Kuramoto model where synchronization occurs gradually.
Explosive ‘higher-order’ Kuramoto model
Mathematician Christiaan Huygens first identified synchronization in 1665 when he observed that two pendulum clocks suspended from the same wooden beam swung in time with each other. However, it wasn’t until 1974 that a simple mathematical model to describe this collective phenomenon was proposed by Japanese physicist Yoshiki Kuramoto.
Kuramoto’s model captures synchronisation in a large network where each node hosts a clock-like oscillator, which is coupled to other oscillators on neighbouring nodes. In the absence of links between the nodes each oscillator obeys its own dynamics and is unaffected by its neighbours. However, when the interaction among neighbour nodes switches to above a given value, the oscillators start to beat at the same frequency.
While the Kuramoto model describes synchronization of dynamics associated with the nodes of a network, in simplicial complexes higher-order objects in the network, such as links or triangles, can also exhibit dynamic or ‘topological’ signals such as fluxes.
In the new study, the researchers propose a higher-order Kuramoto model that can describe synchronization of these topological signals. As topological signals, such as fluxes, can be found in the brain and in biological transport networks the researchers suggest this new model could reveal higher-order synchronization that has previously gone unnoticed.
Professor Bianconi, lead author of the study, said: “We combined Hodge theory, an important branch of topology, with the theory of dynamical systems to shed light on higher-order synchronization. With our theoretical framework, we can treat synchronization of topological dynamical signals associated with links, like fluxes, or to triangles or to other higher-order building blocks of higher-order networks. These signals can undergo synchronization, but this synchronization can be unnoticed if the correct topological transformations are not performed. What we propose here is the equivalent of a Fourier transform for topological signals that can reveal this transition in real systems such as the brain”.
The discontinuous transition found by the study suggests that the synchronization phenomenon is not only spontaneous but emerges abruptly, revealing how topology can induce dramatic changes in the dynamics at the onset of the synchronization transition.
More information
- Research publication: ‘Explosive higher-order Kuramoto dynamics on simplicial complexes’ Millán, A.P., Torres, J.J. and Bianconi, G. (2020), Physical Review Letters. DOI: 1103/PhysRevLett.124.218301
Figure Caption: Schematic representation of a simplicial complex capturing higher-order interactions and sustaining topological signals (on the left) and evidence for explosive synchronization in higher-order Kuramoto model (on the right).