Having a paper published is a fantastic achievement, but particularly so early on in an academic career. MSc student Jun Yamamoto has recently had a paper published in Physical Review E, a journal that covers statistical, nonlinear, biological, and soft matter physics.
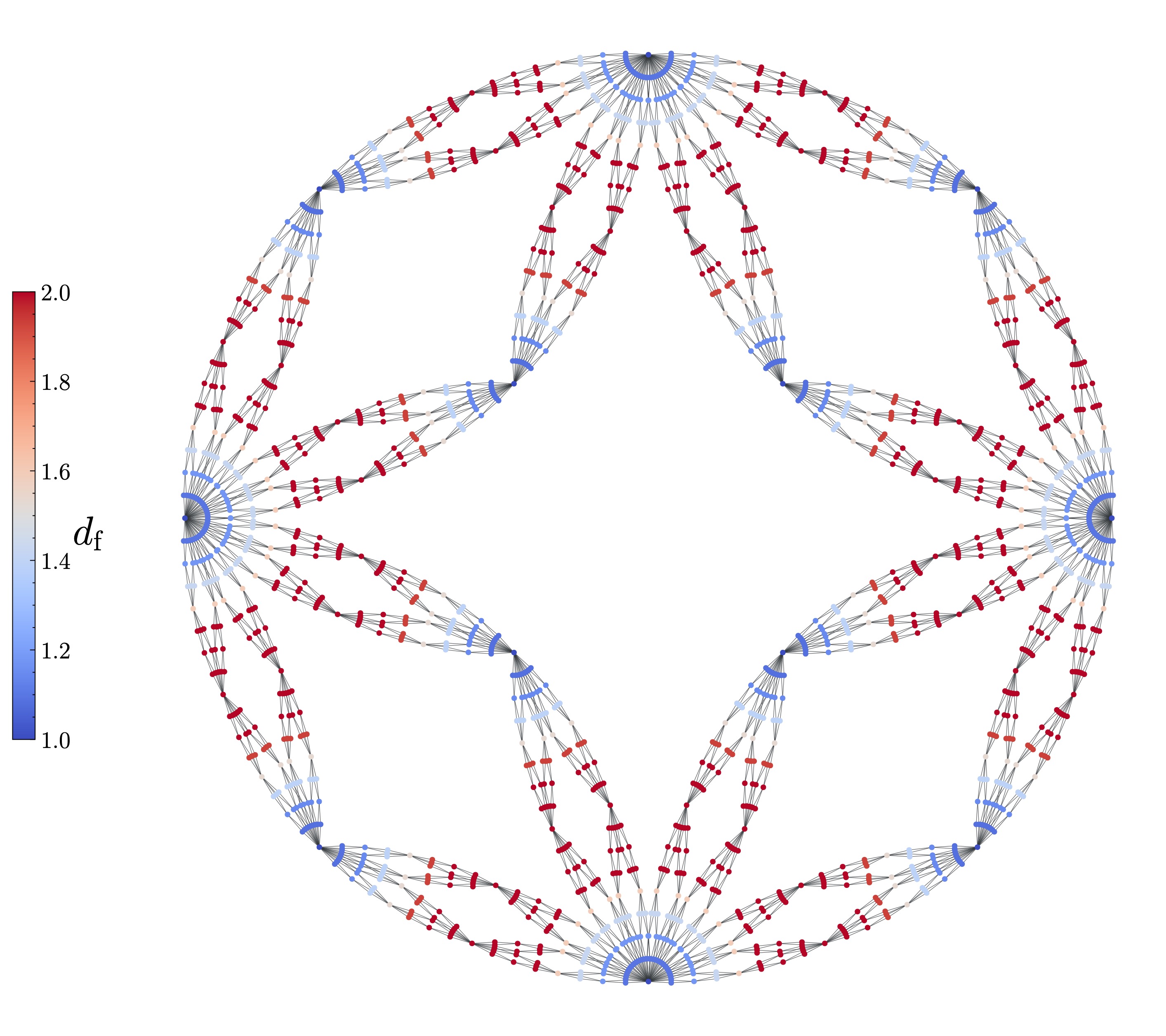
A diagram showing the distribution of local fractal dimensions
The paper titled 'Bifractality of fractal scale-free networks' was co-written with Kousuke Yakubo (Hokkaido University). Having been interested in network structures with strong (long-range) degree correlations, they investigated fractal scale-free networks as mathematically tractable examples of strongly degree-correlated scale-free networks.
Continue reading below for Jun's overview of the research.
A complex network is a representation of the underlying structure of a complex system in which components and their pairwise interactions are respectively depicted as nodes and links. The surge in available big data from social, technological, and biochemical systems around the turn of the century led to an explosion in the number of studies into the structural and dynamical properties of complex networks. Extensive research over the course of a quarter century has revealed that many networks, such as the World Wide Web, protein interaction and actor collaboration networks, possess the scale-free property, in which degree, the number of connections of a node, has a highly heterogeneous distribution with no characteristic degree.
In addition to the scale-free property, many networks representing the real world exhibit strong degree correlations across long network distances. Among such long-range correlated scale-free networks, we were particularly interested in fractal scale-free networks (FSFNs) which possess the scale invariance with respect to network distance. In FSFNs, there exists a degree correlation where high-degree hub nodes stay distant from one another. While long-range degree-correlated networks are in general mathematically challenging to handle, fractal networks are more tractable due to their symmetry of the scale invariance.
By investigating three types of extensive mathematical models of FSFNs and some real-world FSFNs, we have demonstrated that all the considered networks show the bifractal property, where the network structure is characterised by two distinct local fractal dimensions. From our comprehensive exploration, we proposed a new conjecture that any FSFN possesses the bifractal property. Further, we have also identified that the two local dimensions in a bifractal network describe the structures near hubs (infinitely high-degree nodes) and near non-hub nodes (finite degree nodes) that are infinitely apart from hubs when the network size is infinite.
Our conjecture suggests the existence of two types of local dynamical behaviours in FSFNs, such as information diffusion and infection spread. Furthermore, the previously reported qualitative distinctions in various properties between hub and non-hub vicinities could potentially be elucidated from the perspective of bifractality.
The full paper is available on Physical Review E's website.