Mathematicians develop new theory to explain real-world randomness
Einstein’s theory of Brownian motion, which describes the random movement of particles in fluids, is widely used to model randomness throughout science. However, this revolutionary model only works when a fluid is static, or at equilibrium.
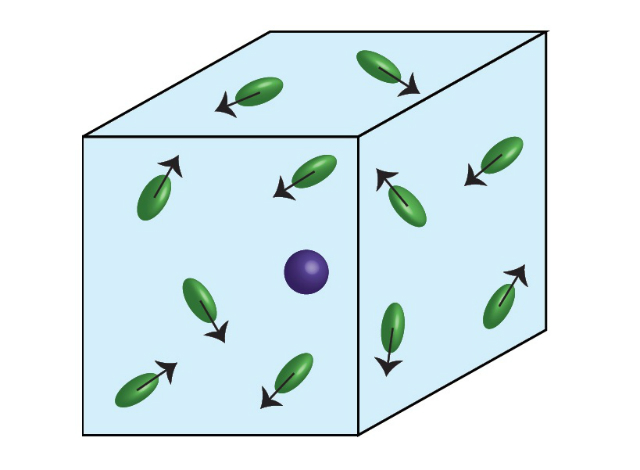
Schematic of the microscopic interactions between active particles (green) and a passive tracer (blue)
In real-life environments, fluids often contain particles that move by themselves, such as tiny swimming microorganisms. These self-propelled swimmers can cause movement or stirring in the fluid, which drives it away from equilibrium.
Experiments have shown that non-moving ‘passive’ particles can exhibit strange, loopy motions when interacting with ‘active’ fluids containing swimmers. Such movements do not fit with the conventional particle behaviours described by Brownian motion and so far, scientists have struggled to explain how such large-scale chaotic movements result from microscopic interactions between individual particles.
Now researchers from Queen Mary University of London, Tsukuba University, École Polytechnique Fédérale de Lausanne and Imperial College London, have presented a novel theory to explain observed particle movements in these dynamic environments.
They suggest the new model could also help make predictions about real-life behaviours in biological systems, such as the foraging patterns of swimming algae or bacteria.
Dr Adrian Baule, Senior Lecturer in Applied Mathematics at Queen Mary University of London, who managed the project, said: “Brownian motion is widely used to describe diffusion throughout physical, chemical and biological sciences; however it can’t be used to describe the diffusion of particles in more active systems that we often observe in real life."
A new model to match experimental observations
By explicitly solving the scattering dynamics between the passive particle and active swimmers in the fluid, the researchers were able to derive an effective model for particle motion in ‘active’ fluids, which accounts for all experimental observations.
Their extensive calculation reveals that the effective particle dynamics follow a so-called ‘Lévy flight', which is widely used to describe ‘extreme' movements in complex systems that are very far from typical behaviour, such as in ecological systems or earthquake dynamics.
Dr Kiyoshi Kanazawa from the University of Tsukuba, and first author of the study, said: “So far there has been no explanation how Lévy flights can actually occur based on microscopic interactions that obey physical laws. Our results show that Lévy flights can arise as a consequence of the hydrodynamic interactions between the active swimmers and the passive particle, which is very surprising."
Future applications in biology and beyond
The team found that the density of active swimmers also affected the duration of the Lévy flight regime, suggesting that swimming microorganisms could exploit the Lévy flights of nutrients to determine the best foraging strategies for different environments.
Dr Baule added: “Our results suggest optimal foraging strategies could depend on the density of particles within their environment. For example, at higher densities active searches by the forager could be a more successful approach, whereas at lower densities it might be advantageous for the forager to simply wait for a nutrient to come close as it is dragged by the other swimmers and explores larger regions of space.
“However, this work not only sheds light on how swimming microorganisms interact with passive particles, like nutrients or degraded plastic, but reveals more generally how randomness arises in an active non-equilibrium environment. This finding could help us to understand the behaviour of other systems that are driven away from equilibrium, which occur not only in physics and biology, but also in financial markets for example.”
English botanist Robert Brown first described Brownian motion in 1827, when he observed the random movements displayed by pollen grains when added to water.
Decades later the famous physicist Albert Einstein developed the mathematical model to explain this behaviour, and in doing so proved the existence of atoms, laying the foundations for widespread applications in science and beyond.
More information
- Research paper: 'Loopy Lévy flights enhance tracer diffusion in active suspensions.' K Kanazawa, T Sano, A Cairoli, and A Baule. Nature. DOI: 10.1038/s41586-020-2086-2
- Study Maths at Queen Mary
Related items

4 August 2025
For media information, contact:
Sophie McLachlanFaculty Communications Manager (Science and Engineering)
email: sophie.mclachlan@qmul.ac.uk

